傅里叶变换的基本概念

从时域到频域的转换 - 解析信号的频率结构

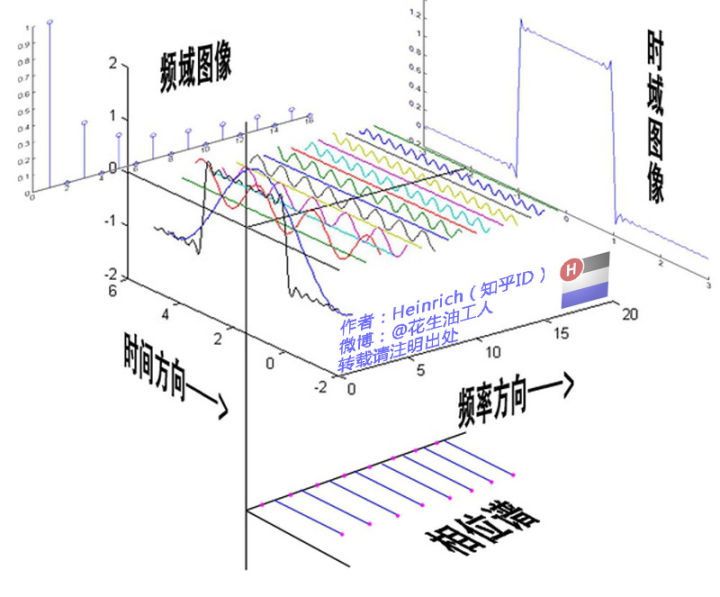
傅里叶变换是一种将时域信号（随时间变化的信号）转换为频域表示（不同频率的叠加）的数学工具，揭示了信号中隐藏的频率成分，为我们提供了观察信号的全新视角。

连续傅里叶变换

F(ω) = ∫_-∞^∞ f(t)e^-jωt dt

离散傅里叶变换

X[k] = Σ_n=0^N-1 x[n]e^-j2πkn/N

时域 (Time Domain)

随时间变化的信号

f(t) 表示信号随时间t的变化

频域 (Frequency Domain)

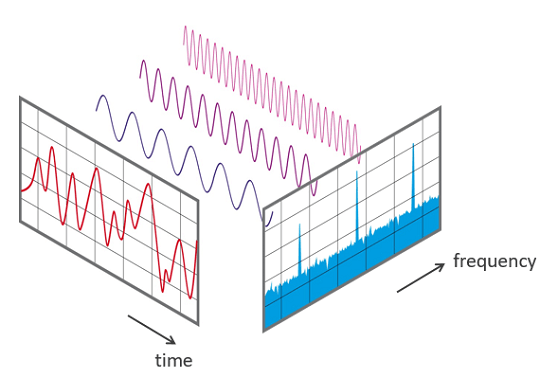
信号的频率组成

F(ω) 展示各频率ω上的能量分布

核心思想

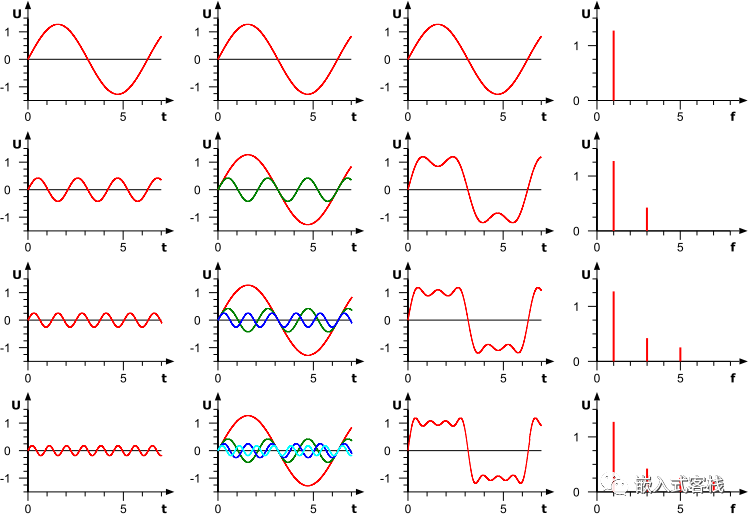
任何周期信号都可以分解为一系列不同频率、振幅和相位的正弦波的叠加，类似于将一首交响乐分解为各种乐器的声音

数学意义

通过积分变换，将时域函数映射到频域，使复杂的时域问题在频域中变得简单，如将卷积运算转化为简单的乘法

变换对象

可应用于连续信号（连续傅里叶变换）、离散信号（离散傅里叶变换）及有限采样序列（离散傅里叶变换DFT及其快速算法FFT）

变换意义

揭示信号的频谱特性，使我们能够识别信号中的重要频率成分、滤除噪声、压缩信息，为信号处理奠定理论基础

"大自然说话用的是数学语言，而其字母就是圆、三角形以及其他数学图形" — 伽利略

傅里叶变换的历史由来

约瑟夫·傅里叶的贡献与发展历程

约瑟夫·傅里叶 (1768-1830)

法国数学家与物理学家

科学家与他的时代

约瑟夫·傅里叶出生于法国革命前夕的动荡时期，曾随拿破仑远征埃及，担任埃及研究院秘书长。在研究热传导问题时，他提出了一项划时代的数学方法——将任意周期函数表示为简单正弦函数的无穷级数。

"热学解析理论"(1822年)一书中，傅里叶首次系统阐述了他的变换理论，虽然当时因其严谨性受到拉格朗日、拉普拉斯等人质疑，但最终改变了数学史和科学史的进程。

傅里叶分析的历史发展

1807年

傅里叶在法国科学院提交论文，提出任何函数都可以用三角函数级数表示，奠定了傅里叶级数的基础

1822年

出版《热的解析理论》，系统阐述了傅里叶级数及其在热传导问题中的应用，开创了数学物理方程的新方法

1867年

数学家洛特·冯·赫姆霍兹拓展了傅里叶的工作，证明了傅里叶级数的收敛性，使理论更加严谨

20世纪初

现代傅里叶分析理论形成，傅里叶变换从热学拓展到量子力学、通信工程等多领域，成为现代科学的基石

1965年

库利和图基发表了快速傅里叶变换(FFT)算法，极大提高了计算效率，促进了傅里叶变换在数字信号处理中的广泛应用

历史意义与学术争议

傅里叶的工作最初引发了数学界的巨大争议，因为它挑战了当时对"函数"概念的认识。他的理论促使数学家重新思考函数的连续性、可微性等基本概念，直接推动了实分析和泛函分析的发展。

从热传导方程到现代信号处理，傅里叶的思想穿越两个世纪，成为连接经典数学与现代科学技术的桥梁，被誉为"历史上最有革命性的数学思想之一"。

"傅里叶变换的美丽在于它将复杂问题简单化，将不可见转化为可见。"

— 现代数学评价

"数学是科学的女王，而数论是数学的女王。" — 高斯

傅里叶变换的数学原理

基本公式与图形化解释

傅里叶变换的核心是将时域信号分解为频域中的正弦波组合，以下是傅里叶变换的数学表达与原理解析：

连续傅里叶变换

F(ω) = ∫_-∞^∞ f(t)e^-jωt dt

正变换：从时域 f(t) 到频域 F(ω)

f(t) = 1/2π ∫_-∞^∞ F(ω)e^jωt dω

逆变换：从频域 F(ω) 回到时域 f(t)

核心要点：

j 为虚数单位，e^-jωt 表示欧拉公式：cos(ωt) - j·sin(ωt)
F(ω) 的模值 |F(ω)| 表示频率 ω 处的振幅谱
F(ω) 的相角 arg[F(ω)] 表示频率 ω 处的相位谱

离散傅里叶变换 (DFT)

X[k] = Σ_n=0^N-1 x[n]e^-j2πkn/N

正变换：从离散时域序列 x[n] 到频域序列 X[k]

x[n] = 1/N Σ_k=0^N-1 X[k]e^j2πkn/N

逆变换：从频域序列 X[k] 回到时域序列 x[n]

计算效率：

直接计算 DFT 需要 O(N²) 运算复杂度
快速傅里叶变换 (FFT) 将复杂度降至 O(N·log N)
FFT 是现代数字信号处理的基础算法之一

图形化解释

上图展示了一个复杂信号（黑色）如何由多个不同频率的正弦波（彩色）组合而成。傅里叶变换正是揭示了这些组成成分的频率、振幅和相位。

重要数学性质

线性性质

α·f₁(t) + β·f₂(t) ⟷ α·F₁(ω) + β·F₂(ω)

时移性质

f(t-t₀) ⟷ F(ω)·e^-jωt₀

频移性质

f(t)·e^jω₀t ⟷ F(ω-ω₀)

时域卷积定理

f₁(t) * f₂(t) ⟷ F₁(ω) · F₂(ω)

时域卷积对应频域相乘

频域卷积定理

f₁(t) · f₂(t) ⟷ (1/2π) · F₁(ω) * F₂(ω)

时域相乘对应频域卷积

经典傅里叶变换对

矩形脉冲 rect(t)

⟷

sinc 函数 (sin(ωT/2)/(ωT/2))

高斯函数 e^-at²

⟷

高斯函数 (√(π/a))·e^-ω²/(4a)

单位冲激函数 δ(t)

⟷

常数 1

深刻洞见

傅里叶变换揭示了信号在时域和频域之间的对偶性，二者是同一信息的不同表现形式。它使我们可以在最适合的域中处理信号——许多复杂的时域操作（如卷积）在频域中变成简单的运算（如乘法）。这一特性使傅里叶变换成为信号处理、波动方程求解和量子力学中不可或缺的数学工具。

"在数学的花园里，傅里叶变换是最美丽的花朵之一。" — 拉普拉斯

傅里叶变换的广泛应用场景

从信号处理到图像分析的多领域应用

傅里叶变换作为一种强大的数学工具，已深入应用于现代科学技术的各个领域，彻底改变了我们理解和处理信息的方式：

信号处理

通过分析频谱成分，可以进行信号滤波、压缩和还原

移除信号中的噪声（低通、高通和带通滤波器）
音频压缩（MP3等压缩算法的基础）
雷达和声纳信号分析

图像处理

将二维图像转换到频域，进行增强和分析

图像压缩（JPEG格式的核心技术）
图像增强和修复（去模糊、去噪声）
边缘检测和特征提取
医学图像处理（CT、MRI扫描）

通信技术

现代通信系统的基础

调制解调技术（无线电、电视与手机信号）
频分复用（OFDM - 4G/5G通信的关键技术）
频谱分析与管理
网络数据传输与WiFi

OFDM 正交频分复用技术原理

科学研究

在多个学科中的深入应用

量子力学（波函数分析）
光学（衍射和干涉现象）
地震学（地震波分析）
天文学（宇宙微波背景辐射分析）
生物医学（脑电图、心电图分析）

"傅里叶变换的美在于它能通过数学视角揭示自然界中的频率模式，从原子振动到星系旋转，无处不在。"

音频处理

均衡器、音效处理、语音识别

计算机视觉

人脸识别、目标检测、场景分析

数据科学

时间序列分析、数据压缩、模式识别

傅里叶变换的跨学科影响

傅里叶变换从最初解决热传导问题，发展为现代信息科学的基石。这种数学工具让我们能够将复杂信号分解为基本组成部分，在时域和频域之间自由切换，极大地推动了科学技术的发展，成为连接纯数学理论与实际工程应用的桥梁。

"最有效的数学工具往往能超越其最初的应用领域，傅里叶变换正是其中的杰出代表。"

傅里叶变换的重要性

现代科技的基石与未来发展的引擎

傅里叶变换在现代科技中的影响

从理论数学到实际应用

数字革命

傅里叶变换是数字信号处理的核心，支撑了现代计算机、智能手机和互联网技术的发展，没有它就没有当今的数字世界。

通信变革

从4G/5G移动通信到卫星传输，傅里叶变换使高效率、大带宽的信息传输成为可能，彻底改变了人类交流方式。

医疗突破

医学成像（CT、MRI）、心电图分析等现代医疗技术都依赖于傅里叶变换，显著提高了疾病诊断和治疗的准确性。

科学理论的基石

傅里叶变换不仅是一个数学工具，更是一种思维方式，它贯穿于量子力学、相对论、宇宙学等现代物理学理论，成为理解自然界基本规律的关键。通过将复杂现象分解为基本组成部分，它提供了简化科学问题的普适方法，被誉为"20世纪最重要的数学发现之一"。

未来科技展望

人工智能中的深度学习算法优化，加速模型训练和推理
量子计算中的量子态分析与量子信息处理
新一代通信技术（6G）中的频谱资源优化与管理
气候模型与精准天气预报，提高对极端气象事件的预警能力

关键启示

傅里叶变换告诉我们，复杂系统往往可以分解为更简单的组成部分，这一思想已经超越了数学和物理学，成为解决复杂问题的普遍方法论。

谢谢观看

从约瑟夫·傅里叶到现在，200年的理论发展与应用创新持续改变着世界